This post is from our friend and colleague Kathy Minas, a 4th grade teacher at PS 158, and an avid strings enthusiast.
Recently, our fourth grade team met with Math in the City co-director and staff developer Kara Imm, who has been working with our school for several years. We wanted to explore ways to introduce Common Core 4th grade standards of measurement and conversion by using strings. What follows is the string we designed together and my notes about how to lead it with kids.
Why this string? Why a ratio table?
The purpose of this string is to introduce students to conversions, using the most common units of measurement, inches and feet. We wanted to ensure that students had a familiar model that visually captured the (twelve-to-one) relationship between these units, which led us to using the ratio table. Our students have worked with the ratio table before in both our multiplication and division units of study. The model allowed them to represent and maintain the relationship between known units in order to multiply, divide, break apart, or even add groups with ease.
Performing measurement conversions on a ratio table also supported students to monitor the reasonableness of their answers. In addition, it encouraged them to keep the relationship between units in mind. Instead of memorizing whether they needed to multiply or divide feet to get inches, they simply trusted the existing relationships on the table that we build together. In fact, student were much more flexible about how to convert and did not rely on a memorized rule or catchy mnemonic to solve these problems.
Tips for leading the string:
We build ratio table together with the class, instead of revealing the entire completed ratio table all at once. We add values to the ratio table — one at a time, increasingly more complex — and ask students to determine the corresponding number of inches or feet. Some values are added to the ratio table as students explain their process.
The string:
Begin by naming a true statement to ground the conversation:
Mathematicians, we know that there are 12 inches in one foot.
Draw a ratio table and label the columns, number of inches and number of feet. If this piece of social knowledge is not known by your students, having a 12-inch ruler to see and touch is also useful at this moment.
Since we know that there are 12 inches in one foot, how many inches are there in 3 feet? How do you know?
Student responses may include:
- I know that there are 12 inches in one foot, so there are 36 inches in 3 feet because you multiply the number of feet by three, which means you have to multiply the number of inches by three.
Note: In order to move away from additive reasoning on the ratio table — also known as repeated addition or “chunking” — I purposely do not record the unit rate of 12 inches in 1 foot on the table until the students bring it up as part of their reasoning. I’m nudging students from additive to multiplicative reasoning on the ratio table. You may wish to ask students to visualize three feet, “What does this look like? What does this make you think of?”

A fourth grader (and sports enthusiast) in my class introduced the unit of a yard immediately, so I added it as a third column to the ratio table and made a post it note  about his unique contribution. I left the yards column blank for most of the string, but then we returned to it later to reason about this third unit.
about his unique contribution. I left the yards column blank for most of the string, but then we returned to it later to reason about this third unit.
Mathematicians, how many feet are there in 60 inches? How do you know?
Student responses might sound like:
- I know that there are 12 inches in 1 foot, 60 inches is 5 times greater than 12 inches, so 60 inches are equivalent to 5 feet.
- I know that 36 inches is equivalent to 3 feet, and 60 inches is 24 more inches than 36. 24 inches is equivalent to 2 feet, so I need to add 2 feet to 3 feet and that’s 5 feet.

So, how many feet are there in 72 inches? How do you know?
Students will likely reason:
- I know that 72 inches is 12 more inches than 60 inches, which means I need to add one more foot to 5 feet, which is 6 feet.
- I know that 72 inches is equal to 36 inches times 2, if I double the 36 inches, I have to double the 3 feet.
Follow up question, “How many yards are there in 72 inches or in 6 feet? How do you know?”
Okay, how many inches are there in 9 feet? Can you picture this? What are you thinking?
I heard students say:
- I know that 9 feet is three times 3 feet, so there are 108 inches in 9 feet because I have to triple 36 inches.
- I know that 6 feet is 3 feet away from 9 feet, so I need to add 36 more inches to 72 inches, which is 108.
Follow up question, “How many yards are there in 72 inches or in 6 feet? How do you know?”
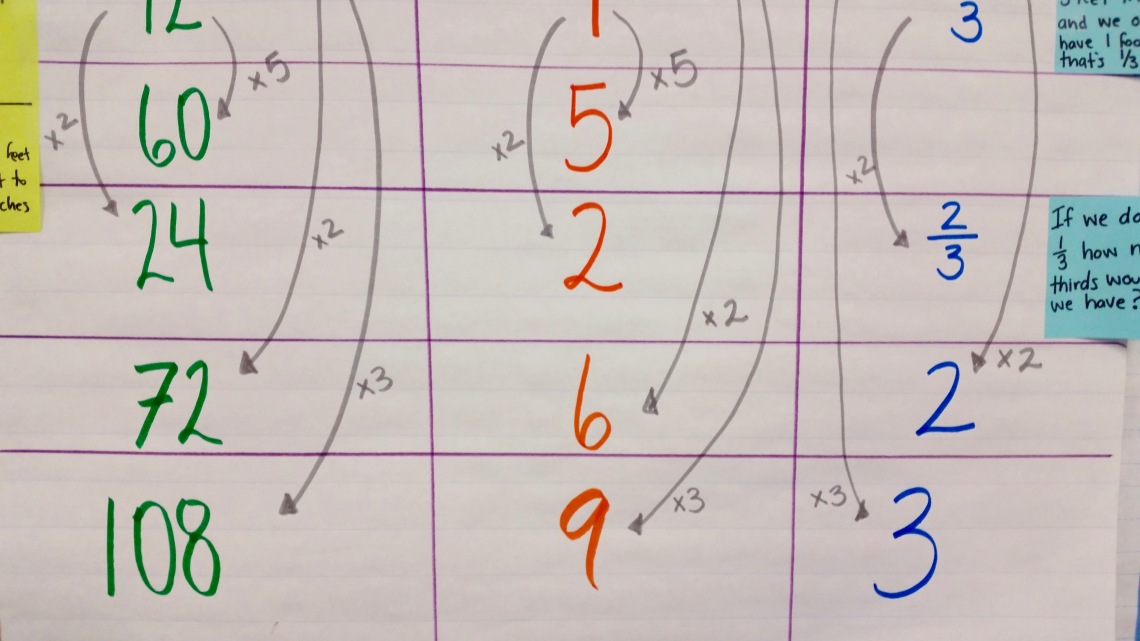
Once we were done with the inches and feet component of the string, we tackled the yards. We returned to the relationship between feet and yards. I asked students to consider,
If we know that there are 3 feet in 1 yard and we only have 1 foot, what part of a whole yard do we have?
Then I asked,
If we have 2 feet, do we have a whole yard yet? What part of a whole yard do we have?
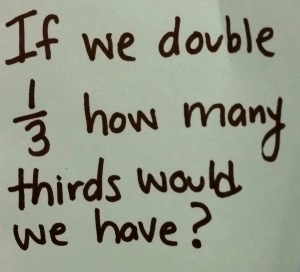
Later I said,
Using all you know about the relationship between feet and yards and all you know about fractions, if we have 5 feet, how many yards do we have?
My students tackled this problem with ease:
- I know that there is 1/3 yard in 1 foot, so there are 5/3 yards in 5 feet.
- So, there is 1 yard in 3 feet and 2/3 yard in 2 feet, which means that in 5 feet there is 1 2/3 yards. I just put them together to make 5.

As big ideas or important strategies come up, my colleagues and I have begun annotating the strings poster so that kids can both see and hear these ideas. I listen carefully for students to make these contributions — we write and display them so that the ideas are shared and accessible to all kids, even if they are still emergent. Sometimes, when students are ready, I nudge kids towards a generalization, which helps us move beyond the specific string and into other related quantities and relationships. Examples of this practice of annotation are below:


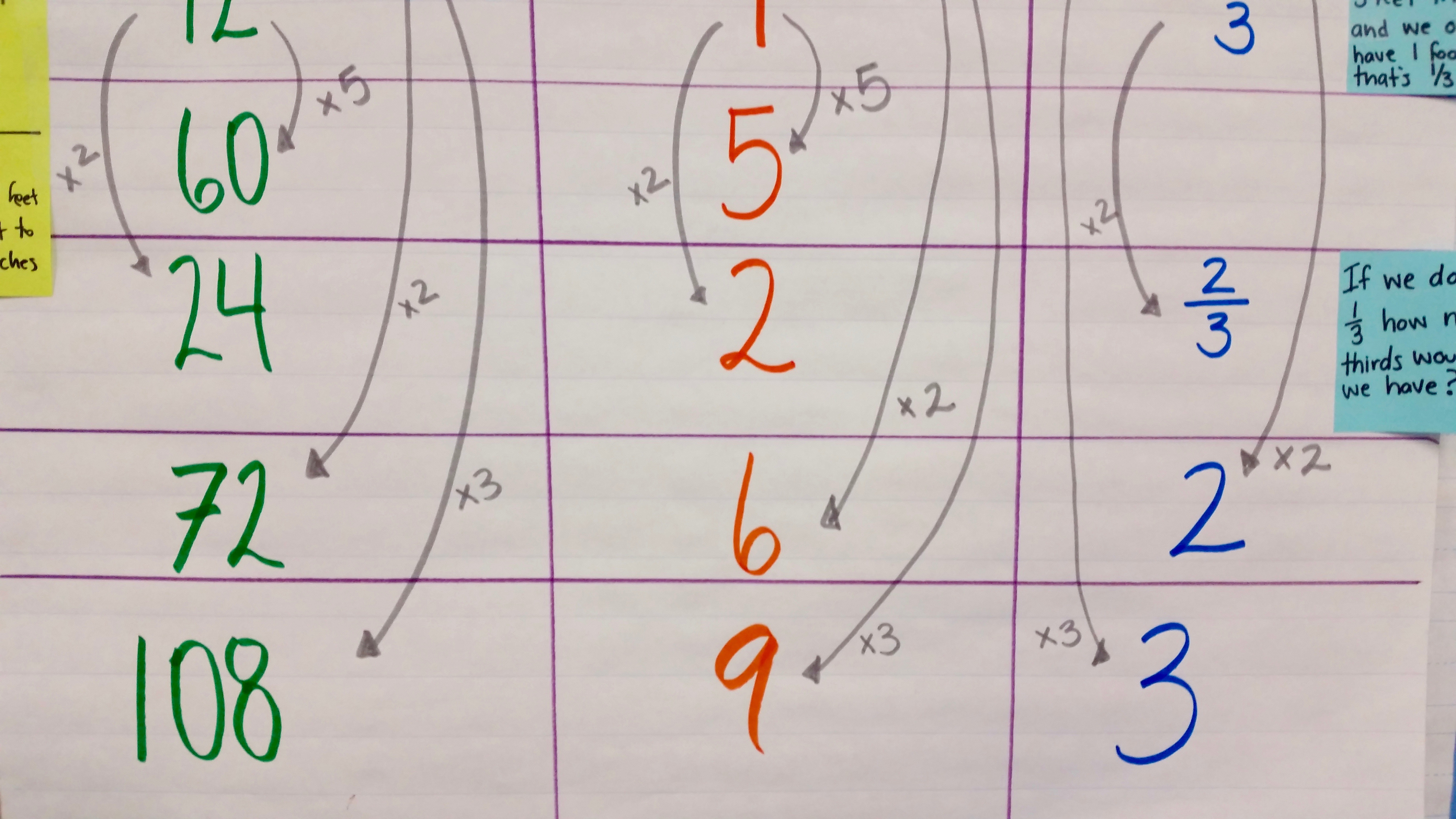


Love it!
I love marking generalizations with a post-it note. Helpful, and moveable!