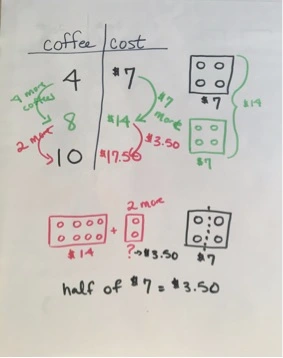
Here’s another important contribution from our friend and colleague Marcelle Good — a 6th grade teacher at School of the … More
Category: ratio table
Feet, inches and yards: Conversions on a ratio table
This post is from our friend and colleague Kathy Minas, a 4th grade teacher at PS 158, and an avid … More
What is the difference between Number Strings and Number Talks?
What’s the difference between a Number String and a Number Talk?
Division of fractions — The role of ratio
A 4th/5th grade teacher I am working with planned to introduce division of fractions and needed some ideas. I … More
Moving straight ahead
Those of you who are fans of the middle school curriculum Connected Math Project (CMP) will especially appreciate this string. … More
Arrays on the West Side
We recently learned that the third grade team at Manhattan School for Children (Elizabeth Frankel-Rivera, Madelene Geswaldo, Alice Hsu and … More
New strings for Measurement + Unit Conversion
Our 5th grade team was trying to address several challenges with implementing Common Core 5th grade standards of multiplying and … More