The following post comes from Rafael Quintanilla, a Mathematics Instructional Coach for the Los Angeles Unified School District and a … More
Category: equivalence
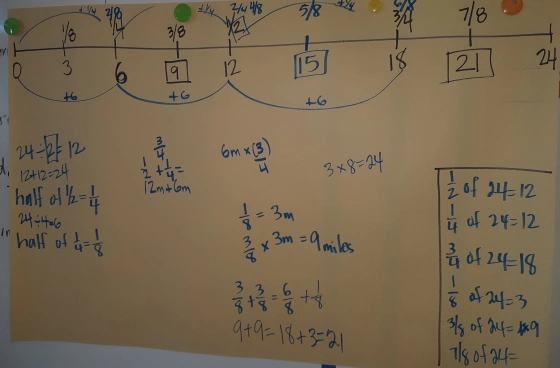
A count around for fractions
This February, I led a Number Strings Writers’ Retreat, as part of my role as staff developer at Math in … More
Number string structure and design
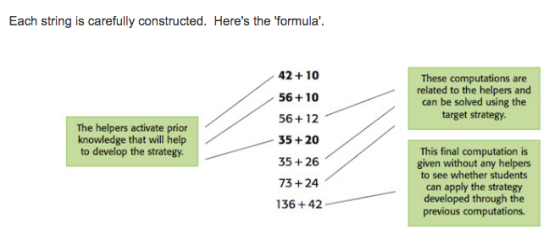
How are number strings designed? Typically, people tend to describe number strings as having the following structure Entry problem Helper … More
Feet, inches and yards: Conversions on a ratio table
This post is from our friend and colleague Kathy Minas, a 4th grade teacher at PS 158, and an avid … More
A “juicy” dilemma
This number string is inspired by an investigation (Comparing and Scaling, Investigation 1.2) from the Connected Math Project curriculum for … More
True False and Fill in the Blank Number Strings for Second Grade
A teacher recently handed me a second grade interim assessment with some true or false and fill in the blank … More