Jenna Laib’s Blog: Daysha at the Board: Assigning Competence

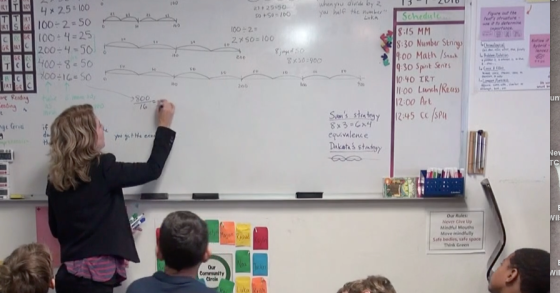
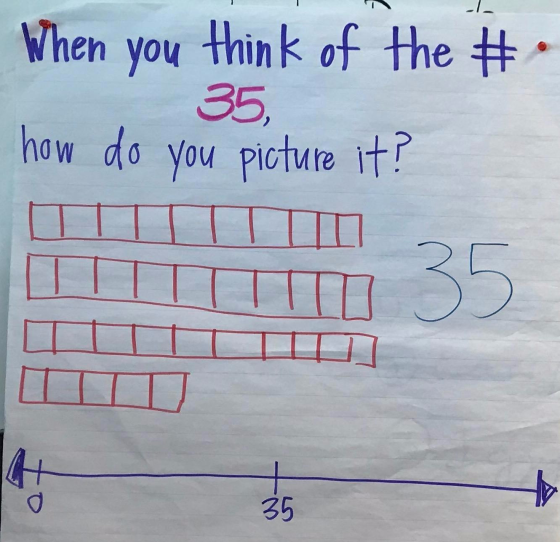https://jennalaib.wordpress.com/2019/03/02/daysha-at-the-board-assigning-competence/ Jenna Laib wrote this post for her blog on a moment in which she was teaching a number string … More

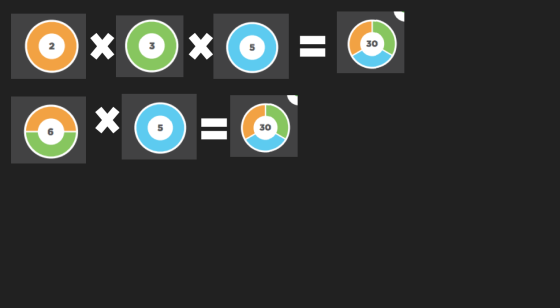
Prime Climb Number String

Last month, I worked in Andrew Eller’s amazing 4th grade classroom in Los Angeles that was beginning an exploration of … More

Differentiating Number Strings: The BandAid Problems

How do you plan a number string for a group of learners who are working on very different skills in … More

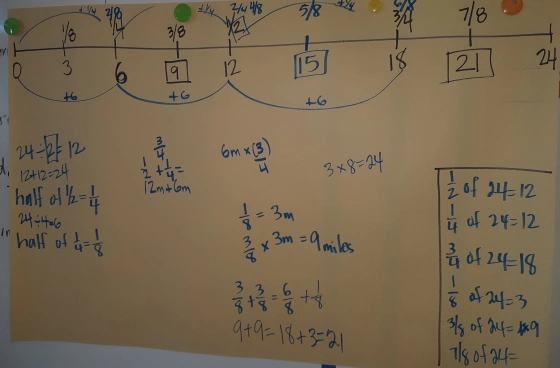
Biking on the fractional number line . . .

The following post comes from Rafael Quintanilla, a Mathematics Instructional Coach for the Los Angeles Unified School District and a … More

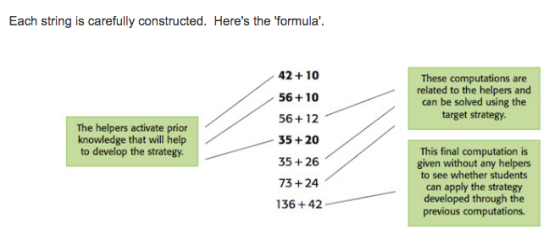
Number string structure and design

How are number strings designed? Typically, people tend to describe number strings as having the following structure Entry problem Helper … More

Video: Division on the open number line in fourth grade

Wondering what a number string looks like in a classroom? Curious about the details of the routine? The following video features … More

What is the difference between Number Strings and Number Talks?

What’s the difference between a Number String and a Number Talk?

Complications with representing constant difference on an open number line

Representing student thinking during a number string is complex. Certain strategies are particularly challenging to represent. For addition and subtraction, … More

Decimal Addition: The Wonders of Friendly Numbers & Compensation

The following post was written by Belinda Paine, an eighth grade special education teacher and one of my credential students. … More

True False and Fill in the Blank Number Strings for Second Grade

A teacher recently handed me a second grade interim assessment with some true or false and fill in the blank … More

30 ways to make number strings more inclusive

As a teacher in inclusive settings, number strings were a critical part of my daily mathematical work.  Routines are highly … More

The delight of disequilibrium

Disequilibrium is Piaget’s term to describe when what a learner already knows comes into conflict with new information. Learners must … More

The “King of Strings” teaches us that strings are maatwerk

I recently reached out to Willem Uittenbogaard. Willem was one of the original collaborators between Math in the City (founded by … More

Photo number strings for multiplication

Here are two photos I snapped as I walked by a 99 cent store in LA. Beautiful arrays, no?  I … More

Go-to questions for teaching number strings

My four-year-old son likes to walk over to the magnetic rekenrek (math rack) I keep on the fridge, move some … More

a series of sorting fractions number strings

Sorting Fractions, money, percentages or decimals Which would you rather have? 45/100 or ½ ¾ or 8/10 8/20 or 2/5 … More