Prime Climb Number String

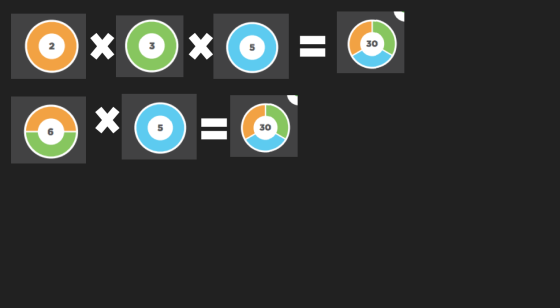
Last month, I worked in Andrew Eller’s amazing 4th grade classroom in Los Angeles that was beginning an exploration of … More

Feet, inches and yards: Conversions on a ratio table

This post is from our friend and colleague Kathy Minas, a 4th grade teacher at PS 158, and an avid … More

Lately, I’ve been seeing arrays everywhere I go: at the grocery store, at the pharmacy, at the farmers’ market. And, … More

Disequilibrium is Piaget’s term to describe when what a learner already knows comes into conflict with new information. Learners must … More

Here’s a string I designed with a team of fifth grade teachers who were looking for creative ways to encourage … More