About Kathy: Kathy Minas is a 5th grade teacher at a public school in Los Angeles. She is an enthusiastic mathematician … More
Category: design of number strings
Number string structure and design
How are number strings designed? Typically, people tend to describe number strings as having the following structure Entry problem Helper … More
Cars, coffee, and climbing stairs: Inviting students into the story
Here’s another important contribution from our friend and colleague Marcelle Good — a 6th grade teacher at School of the … More
Feet, inches and yards: Conversions on a ratio table
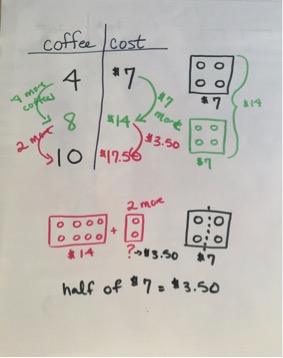
This post is from our friend and colleague Kathy Minas, a 4th grade teacher at PS 158, and an avid … More
Numeracy for high school: A unique challenge
Here’s a conversation between collaborators and friends Kara Imm (Co-Director, Math in the City) and Geoffrey Enriquez (Math Teacher, Vanguard … More
A “juicy” dilemma
This number string is inspired by an investigation (Comparing and Scaling, Investigation 1.2) from the Connected Math Project curriculum for … More
What is the difference between Number Strings and Number Talks?
What’s the difference between a Number String and a Number Talk?
A Number String for Angle Measures — Before We Kick the Bucket
This post was co-created by Jesse Burkett, Ranona Bowers, and Adrian Sperduto — teachers in the Hazelwood School District and … More
What’s in a name?
This post is by reader and strings enthusiast Laura Bofferding, Assistant Professor, Purdue University I was first introduced to number … More
(Re)Thinking Context
A recent conversation between two New York City math educators, Carol Mosesson-Teig and Kara Imm Kara, I have been thinking … More
Moving straight ahead
Those of you who are fans of the middle school curriculum Connected Math Project (CMP) will especially appreciate this string. … More
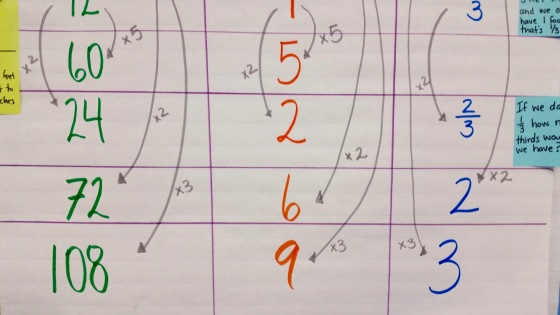
New percentage number strings
We recently saw the problem above on a New York CCSS-M 6th grade benchmark test. A few teachers I was … More
The “King of Strings” teaches us that strings are maatwerk
I recently reached out to Willem Uittenbogaard. Willem was one of the original collaborators between Math in the City (founded by … More
Challenge problems, helper problems
When designing strings, there are typically one or more helper problems before a challenge problem. For example, you might start … More
The Power of Strings
I’m embarrassed to say this, I have a vivid memory of around my fourth year of teaching 5th grade and … More