1. Be explicit at the start that getting more voices, more ideas into our conversation is our goal, because we … More
Author: Kara Imm
I am a K-12 math educator and design thinker, based in New York City, who works closely with teachers, leaders and teams across the country and beyond. In addition, I love writing and designing with teachers about the persistent and "tricky" issues we face in the project of teaching and learning mathematics.
Redesigning math communities for distance learning
About Kathy: Kathy Minas is a 5th grade teacher at a public school in Los Angeles. She is an enthusiastic mathematician … More
Keeping our math communities humming
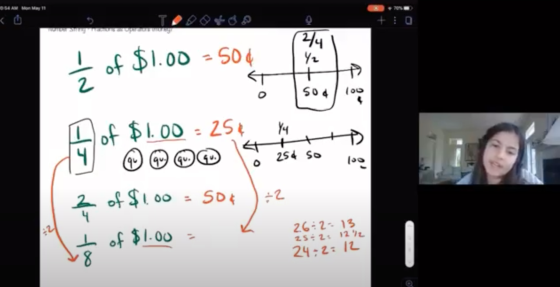
In this post, Kara Imm shares a May 2020 interview with Kate Smallberg about how to transition our number strings … More
Learning to “trust the ten”—Developing a community of first grade mathematicians
Teacher-author Lindsay Pardeck is in her 7th year of teaching first grade at Eureka Elementary in the Rockwood School District. … More
The Mathematics of Core Sampling: Division of Fractions
About the Co-Authors Keely Zaientz and Corey Levin teach 6th and 8th grade math in an integrated co-teaching classroom at … More
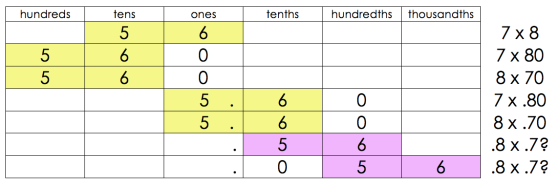
Trusting the digits: Developing place value understanding
For several years, across various school communities, a teacher will tell me, “My kids don’t really have a strategy for … More
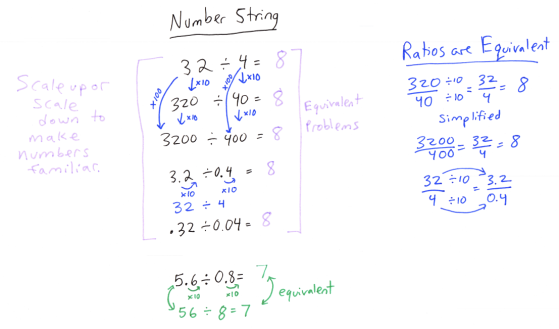
Life beyond the algorithm: Division of decimals
About the author: Kit Golan Kit is an MfA Master Teacher teaching 6th and 7th grade math in a NYC … More
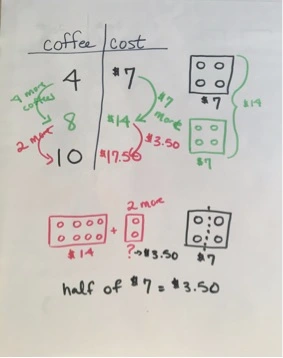
Cars, coffee, and climbing stairs: Inviting students into the story
Here’s another important contribution from our friend and colleague Marcelle Good — a 6th grade teacher at School of the … More
Feet, inches and yards: Conversions on a ratio table
This post is from our friend and colleague Kathy Minas, a 4th grade teacher at PS 158, and an avid … More
Numeracy for high school: A unique challenge
Here’s a conversation between collaborators and friends Kara Imm (Co-Director, Math in the City) and Geoffrey Enriquez (Math Teacher, Vanguard … More
A “juicy” dilemma
This number string is inspired by an investigation (Comparing and Scaling, Investigation 1.2) from the Connected Math Project curriculum for … More
So, what’s the story?
This number string attempts to do something a little different — it begins with the model (instead of the problem), … More
On the rug with Angela
It’s late in the school year and I’m sitting on the edge of the rug in Angela Fiorito’s 1st grade … More
Why Conjectures Matter
This post is from our colleague and friend William Deadwyler, a 6th grade math teacher and strings enthusiast who works … More
What the kids say…..
I’ve known Rachel Carr for many, many years. She shepherded me through that exhilarating and exhausting first year of teaching … More
Beyond Skip Counting
This post comes to us from strings enthusiast and middle school teacher Marcelle Good, who works at School of the … More
Number Strings 