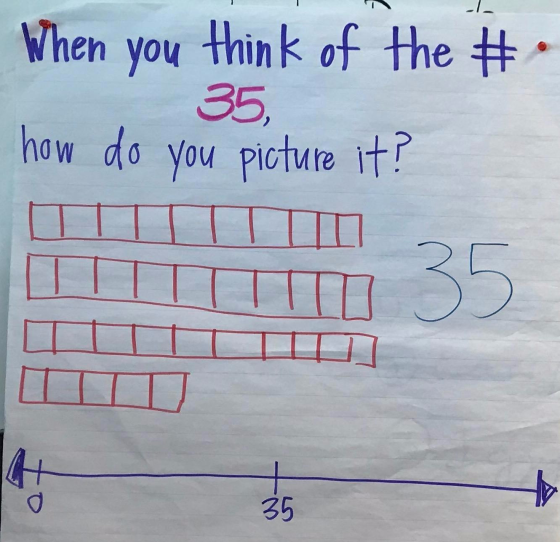Teacher-author Lindsay Pardeck is in her 7th year of teaching first grade at Eureka Elementary in the Rockwood School District. … More
Category: use of context
Differentiating Number Strings: The BandAid Problems
How do you plan a number string for a group of learners who are working on very different skills in … More
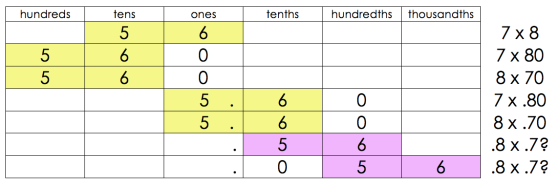
Trusting the digits: Developing place value understanding
For several years, across various school communities, a teacher will tell me, “My kids don’t really have a strategy for … More
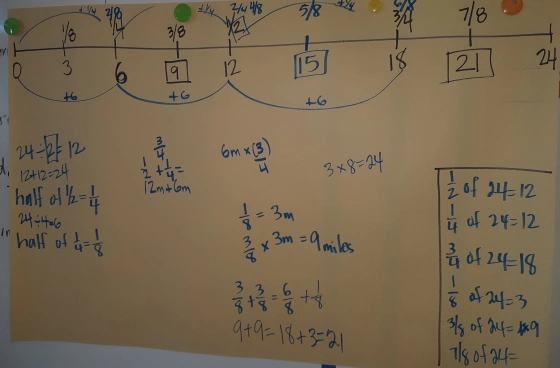
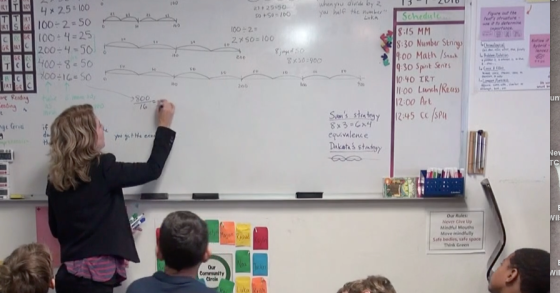
Biking on the fractional number line . . .
The following post comes from Rafael Quintanilla, a Mathematics Instructional Coach for the Los Angeles Unified School District and a … More
A count around for fractions
This February, I led a Number Strings Writers’ Retreat, as part of my role as staff developer at Math in … More
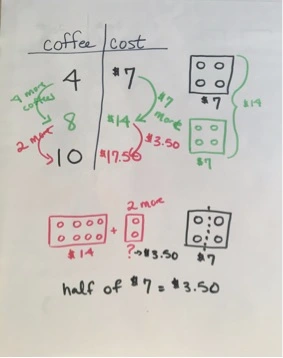
Cars, coffee, and climbing stairs: Inviting students into the story
Here’s another important contribution from our friend and colleague Marcelle Good — a 6th grade teacher at School of the … More
Video: Division on the open number line in fourth grade
Wondering what a number string looks like in a classroom? Curious about the details of the routine? The following video features … More
A “juicy” dilemma
This number string is inspired by an investigation (Comparing and Scaling, Investigation 1.2) from the Connected Math Project curriculum for … More
So, what’s the story?
This number string attempts to do something a little different — it begins with the model (instead of the problem), … More
30 ways to make number strings more inclusive
As a teacher in inclusive settings, number strings were a critical part of my daily mathematical work. Routines are highly … More
Chocolate Arrays
Lately, I’ve been seeing arrays everywhere I go: at the grocery store, at the pharmacy, at the farmers’ market. And, … More
A Number String for Angle Measures — Before We Kick the Bucket
This post was co-created by Jesse Burkett, Ranona Bowers, and Adrian Sperduto — teachers in the Hazelwood School District and … More
(Re)Thinking Context
A recent conversation between two New York City math educators, Carol Mosesson-Teig and Kara Imm Kara, I have been thinking … More