In this post, Kara Imm shares a May 2020 interview with Kate Smallberg about how to transition our number strings … More
Category: money model
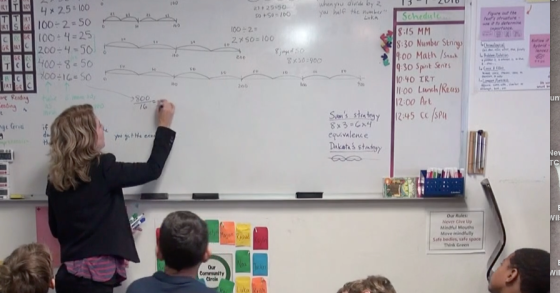
Video: Division on the open number line in fourth grade
Wondering what a number string looks like in a classroom? Curious about the details of the routine? The following video features … More
What the kids say…..
I’ve known Rachel Carr for many, many years. She shepherded me through that exhilarating and exhausting first year of teaching … More
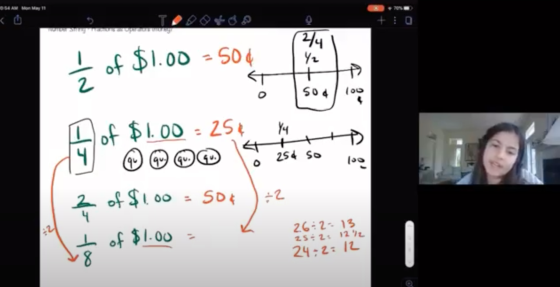
“Stack of Bills” string
Here’s a string I designed with a team of fifth grade teachers who were looking for creative ways to encourage … More
Number Strings 